في كلّ عام يفيض نهر النيل ويغمر الأراضي المجاورة بالكامل، حيث تُمحى كلّ الحدود السابقة التي استُخدِمت للفصل بين مُلكيّات الأراضي، وتتداخل الأمور على الإنسان المصري القديم، الذي كان بحاجة ماسّة إلى البناء وعلم المساحات.
وصفات حسابية بسيطة ابتكرها بُناة الأهرامات
كانت تُلبّى هذه الاحتياجات عبر وصفات علمية مؤلّفة من بضعة خطوات حسابية بسيطة. فقد جاء في برديّة رند أن الإنسان المصري عرف مبرهنة فيثاغور في حالة واحدة، عندما تكون أطوال أضلاع المثلث ثلاث وأربع وحدات، فيكون طول الضلع الثالث (الوتر) خمس وحدات.
أيضًا عرف الإنسان المصري القديم أنّ محيط الدائرة يساوي 32/9 من قطرها، أي إنّه أوجد قيمة مقرّبة بنسبة معقولة للعدد باي π.
وصفات حسابية لدى الشعوب الأخرى
على الجانب الآخر من العالم كان لدى الهنود وصفاتهم الحسابية الخاصّة، فقد عرفوا المثلث القائم في حالة خمس وحدات واثنتا عشرة وحدة، فيكون الوتر ثلاث عشرة وحدة.
وبالرغم من كلّ هذه الاكتشافات والمعرفة، لم تكن هذه الخطوات كافية لولادة الهندسة كعلم مستقلّ يتمتع بالتجانس والتماثل واللانهائية والتجريد والتعميم.
شعبُ واحد امتلك هذه الصفات وهو الإغريق، وخصوصًا طاليس، الذي نجح بسبب معرفته الواسعة بالفلك في اكتشاف لحظة يتساوى فيها الشيء مع ظلّه، استغل طاليس تلك اللحظة لحساب ارتفاع هرم خوفو الهرم الأكبر من بين أهرامات مصر الثلاثة.
بعد طاليس جاء فيثاغور صاحب فكرة العلم، من خلال برهانه لنظريته الشهيرة المعروفة باسمه، نحن لا نعرف كيف برهنها بالضبط، كما يُقال إنّه برهنها بأكثر من طريقة، وسنورد هنا بعض التكهنات لطريقة البرهان.
برهان نظرية فيثاغور
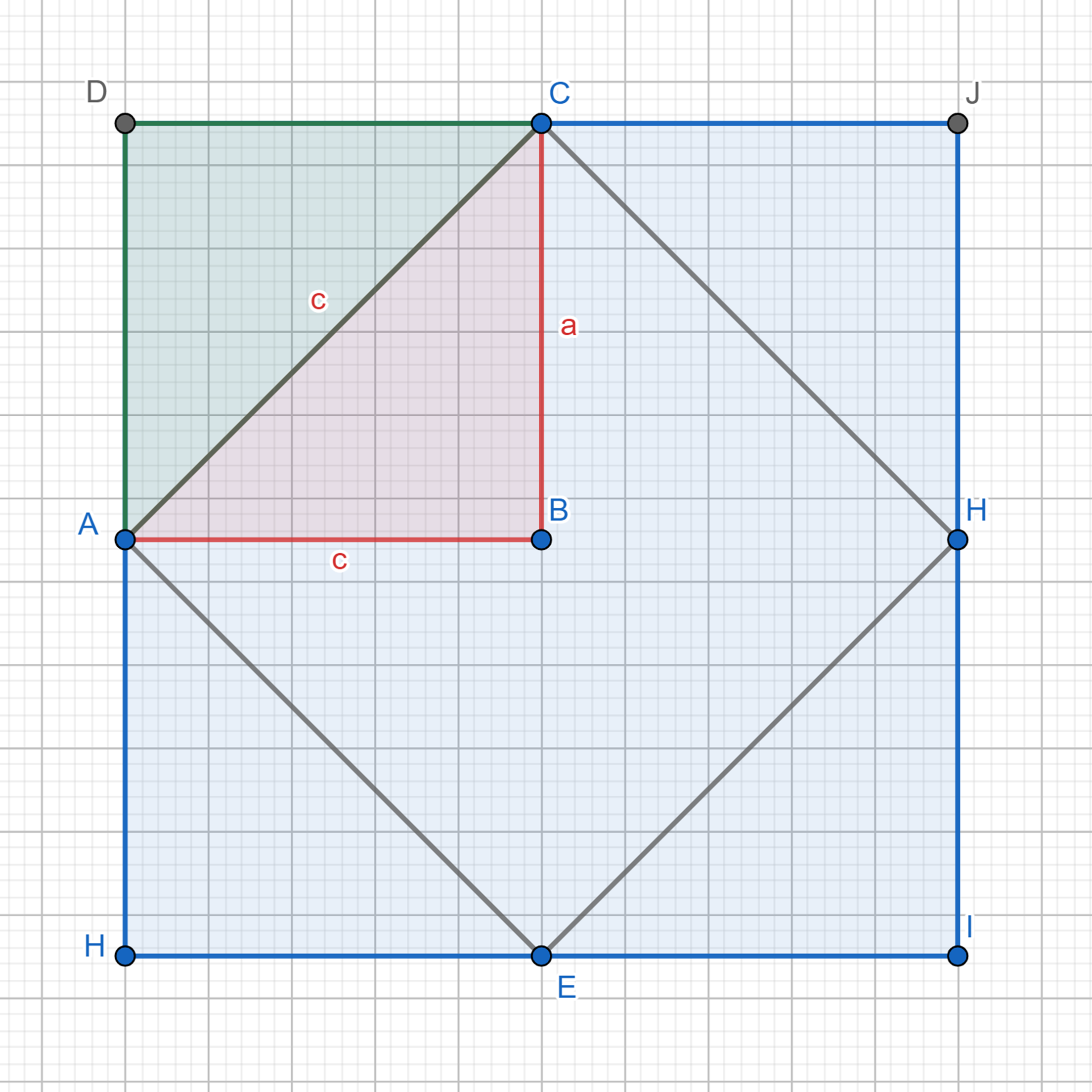
استخدم فيثاغور ورقة مقسّمة إلى وحدات مربّعة متساوية، ورسم المثلث القائم ABC الذي كانت أطوال أضلاعه a,b,c كما هو واضح بالشكل، وكان طولا الضلعين a,b يساوي الواحد لكلّ منهما، بينما طول الوتر c مجهول ونريد حسابه.
لنحسب مساحة المربّع المُنشأ على الضلع b وهو AEHC والتي ستكون بحسب العلاقة التالية:
S(AEHC) = S(DHIJ) – 4.S(DCA)
لكن لدينا
S(ABCD) = 2.S(DCA) = 2.S(ABC)
بالتالي
S(AEHC) = S(DHIJ) – 2.S(ABC) = 4 – 2*1 = 2
يُقال إنّ فيثاغور عندما انتهى من هذا البرهان الإبداعي تقرّب للآلهة بمئة ثور شكرًا لها لأنّه استطاع تعميم نظريته على كلّ المثلّثات القائمة.
نشأة الفيثاغورية
لم تكتمل فرحة فيثاغور وتلاميذه ببرهان النظرية وتعميمها حتى اصطدموا بواقع أنّ العدد 2√ عددًا أصمًا، لا يمكن التعبير عنه بنفس السهولة التي يُعبّر بها عن طول الضلعين القائمين 1 أي بعدد صحيح، فحاولوا الالتفاف عليه بمحاولات شتّى فتارة يقرّبونه لأقرب عدد منطوق وتارة يحصرونه بين سلسلتين من الأعداد، لكنهم يئسوا واعتبروا ذلك عيبًا يجب أن يُوارى، فأبقوا أمره سرًا خوفًا من لعنة الآلهة، وبذلك تأسّست أوّل جمعية سرية في التاريخ، حتى أُشير لها فيما بعد بالجمعية الفيثاغورية، والديانة الفيثاغورية، والفلسفة الفيثاغورية، بالطبع نحن نعدّها من الفلسفات، وهي تحتلّ مكانةً رفيعة بين الفلسفات اللاطبيعية.
ارتقاء الهندسة
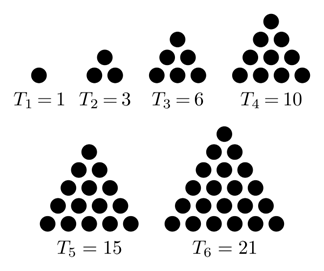
قد يظنّ القارئ أنّ قضية العدد الأصمّ قد أُعطيت حجمًا أكبر ممّا تستحقّ، لكن الواقع أنّها ليست الدافع وراء نشأة جماعة الفيثاغوريين السرية فحسب، بل كانت الترياق الذي أمدّ الهندسة بالحياة، حيث اضطر الفيثاغوريين إلى الحطّ من شأن الأعداد ورفع شأن المفاهيم الهندسية، لدرجة أنّهم صاروا يعبّرون عن الأعداد بطرق هندسية فظهرت لأوّل مرّة الأعداد المثلّثة والأعداد المربّعة والأعداد المستقيمة وغيرها..
انتقل الشعور برقيّ الهندسة وسموّها فوق الأعداد إلى علماء آخرين أهمّهم وأشدّهم أثرًا كان إقليدس أبو الهندسة الإقليدية، صاحب الكتاب الأنجح على مرّ التاريخ كتاب “الأصول” أو “العناصر” الذي وضع فيه أسس الهندسة المستوية وألحق بها بعض الفصول في الحساب.
بقيت الهندسة متربّعةً على عرش الرياضيات بفضل أصول إقليدس قرابة الألفي سنة حتى جاء القرن السابع عشر وما تلاه من إعادة تأسيسٍ للعلوم وعلى رأسها الرياضيات.
الكاتب: د. أحمد خطيب مستشار في مبادرة مسارات