Each year, the Nile River floods, submerging the surrounding lands and erasing the previously marked boundaries used to separate land ownership.
This created a pressing need for the ancient Egyptians, who required knowledge in construction and surveying.
Simple Mathematical Formulas Invented by the Pyramid Builders
These needs were met through scientific formulas consisting of a few simple mathematical steps.
For instance, the Rhind Papyrus indicates that the ancient Egyptians knew of Pythagoras’ theorem in the case of a right triangle with sides of three and four units, where the hypotenuse would be five units.
Additionally, the ancient Egyptians knew that the circumference of a circle is approximately 3 1/7 times its diameter, essentially finding a reasonable approximation for the number π (pi).
Mathematical Recipes from Other Cultures
On the other side of the world, the Indians had their own mathematical recipes, knowing the right triangle in the case of five and twelve units, making the hypotenuse thirteen units.
Despite these discoveries and knowledge, these steps were not sufficient to give birth to geometry as an independent science characterized by cohesion, symmetry, infinity, abstraction, and generalization.
A Singular People Possessed These Qualities:
The Greeks Specifically, Thales, who, due to his extensive knowledge in astronomy, discovered the moment when an object equals its shadow. Thales used this moment to calculate the height of the Great Pyramid of Khufu, the largest of the three Egyptian pyramids.
Following Thales, Pythagoras, the proponent of scientific thought, proved his famous theorem known by his name. While it is not known exactly how he proved it, it is said that he demonstrated it in more than one way. Here, we speculate on one possible method.
Proof of Pythagoras’ Theorem
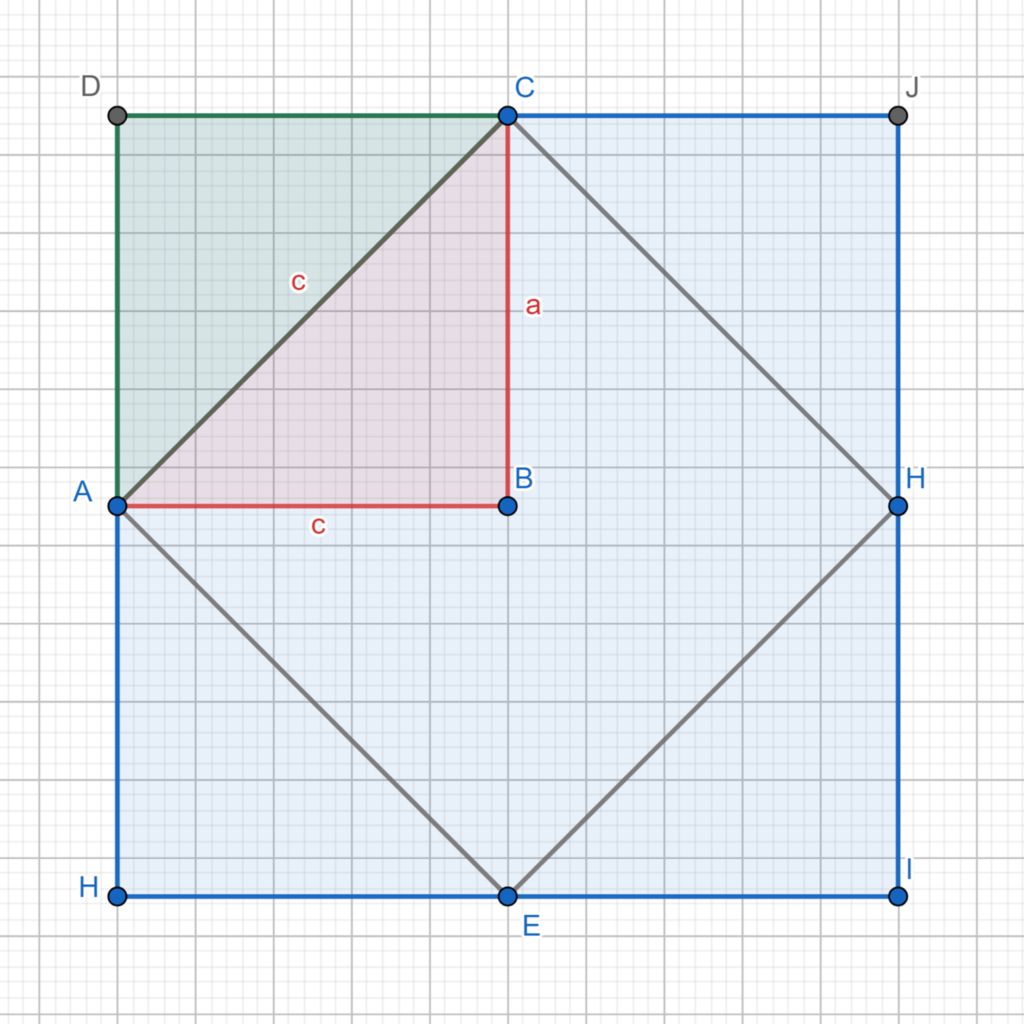
Pythagoras used a sheet divided into equal square units and drew a right triangle, ABC, with side lengths a, b, c, as shown in the diagram.
The lengths of sides a and b were each one unit, while the hypotenuse c was unknown and sought to be calculated.
To calculate the area of square AEHC built on side b, we use the following relationship:
S(AEHC) = S(DHIJ) – 4.S(DCA)
However, we have
S(ABCD) = 2.S(DCA) = 2.S(ABC)
Therefore,
S(AEHC) = S(DHIJ) – 2.S(ABC) = 4 – 2*1 = 2
It is said that when Pythagoras completed this creative proof, he offered a hundred oxen in thanks to the gods for enabling him to generalize his theorem to all right triangles.
The Birth of Pythagoreanism
The joy of Pythagoras and his disciples in proving and generalizing the theorem was short-lived when they encountered the reality that √2 is an irrational number, not easily expressible like the lengths of the other two sides (1), which are integers.
They tried various methods to approximate or confine it between two series of numbers but eventually despaired and considered it a flaw that must be concealed, keeping it secret for fear of divine retribution.
This secrecy led to the establishment of the first secret society in history, later referred to as the Pythagorean society, religion, and philosophy, which is considered a profound philosophical system.
The Rise of Geometry
While it might seem that the issue of the irrational number was overemphasized, it was not only the catalyst for the creation of the secret group of Pythagoreans but also a tonic that infused life into geometry.
This forced the Pythagoreans to de-emphasize numbers and elevate geometric concepts to the extent that they began to express numbers in geometric ways, leading to the introduction of triangular, square, and straight numbers, among others.
The sentiment of the refinement and elevation of geometry above numbers was passed on to other scholars, the most important and influential of whom was Euclid, the father of Euclidean geometry.
He authored the most successful book in history, “The Elements,” in which he established the foundations of plane geometry and appended several chapters on arithmetic.
Geometry remained enthroned at the pinnacle of mathematics thanks to Euclid’s principles for nearly two thousand years, until the 17th century and its subsequent scientific renaissance, with mathematics leading the re-establishment of the sciences.
Author: Dr. Ahmed Khatib, Advisor at Masarat Initiative